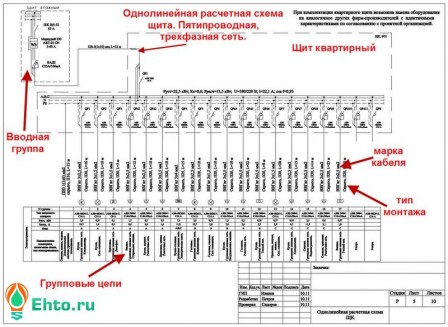
Построение развертки усеченного конуса по начертательной геометрии

Развертка на примере усеченного конуса

Развертку конуса можно получить автоматически используя приложение Оборудование: Развертки, либо построить конус листовым телом и развернуть его. Рассмотрим оба способа.

Построение развертки усеченного конуса, выполненного листовым телом

1. Создадим эскиз на плоскости XY (кликнуть левой кнопкой мыши на плоскость XY и выбрать из всплывающего меню команду «Создать эскиз»);
2. Построим в эскизе окружность произвольного диаметра с центром в начале координат
3. Выйдем из эскиза кликнув по индикатору режима и создадим смещенную от XY плоскость. Расстояние выберем любое.Команда»Смещенная плоскость»размещена на инструментальной панели «Вспомогательные объекты» (размещение команды показано на рисунке). После вызова команды необходимо кликнуть по плоскости XY и задать расстояние на Панели параметров, после чего подтвердить создание плоскости командой «Создать объект» 
4. Создаем на смещенной плоскости эскиз, в эскизе выполняем построение окружности произвольного диаметра с привязкой центра к началу координат (аналогично пунктам 1-2). Выходим из эскиза кликнув левой кнопкой мыши по индикатору режима. В итоге деталь должна иметь следующий вид:
5. Строим усеченный конус командой «Линейчатая обечайка», которая расположена на панели «Элементы листового тела» в наборе «Листовое моделирование».Запустив команду указываем Эскиз1 и Эскиз2, можно указать их в дереве, можно просто кликнуть по окружностям в окне модели. Также требуется задать толщину стенки усеченного конуса на Панели параметров. Для подтверждения создания тела нажимаем кнопку «Создать объект» 
6. Усеченный конус построен, теперь необходимо выполнить его развертку. Для этого воспользуемся командой «Развернуть» с Панели быстрого доступа. После вызова команды кликнем по конической грани и нажмем «Создать объект» . Перейти от развертки к усеченному конусу можно отжав режим развертка
7. Остается перенести данную развертку с 3D в чертеж. Для этого создаем новый документ чертеж. Заходим по пути: Главное текстовое меню — Вставка — Вид с модели — Вид с модели…Указать деталь с разверткой (обязательно файл с деталью сохранить, иначе он не появится в списке). Поставить на Панели параметров галочку «Развертка». В результате будет построен вид с разверткой.

Построение развертки усеченного конуса с помощью приложения

Приложение Оборудование: Развертки позволяет построить развертку деталей имеющих форму:

• усеченного цилиндра;
• прямого кругового конуса;
• усеченного прямого кругового конуса;
• кругового конуса, усеченного не параллельно основанию;
• наклонного кругового конуса, усеченного параллельно основанию;
• тройников;
• перехода с прямоугольного сечения на круглое;
• труб прямоугольного и многоугольного сечения;
• отводов.

Строить развертки поверхностей, имеющих форму типа:

• цилиндра;
• конуса;
• тора;
• сферы.

Приложение Оборудование: Развертки входит в Машиностроительную конфигурацию КОМПАС и приобретается отдельно от базового КОМПАС. Если Машиностроительная конфигурация на Вашем компьютере установлена, требуется подключить Приложение. Для этого нужно зайти по пути: Главное текстовое меню — Приложения — Конфигуратор — раскрыть в списке раздел Оборудование — выделить строку Оборудование:Развертки и нажать на ссылку «Подключить»

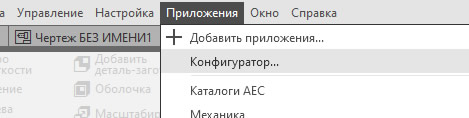
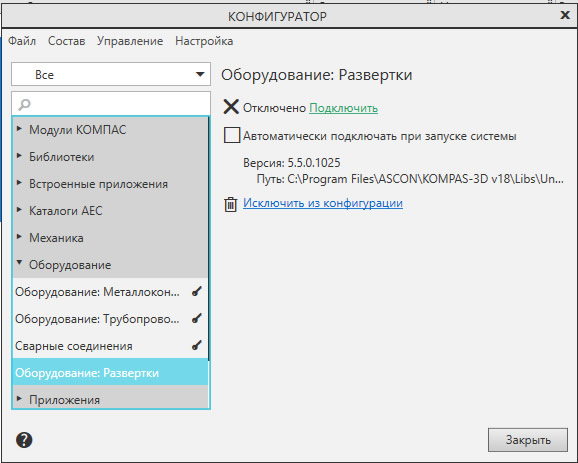
После подключения Приложение появится в наборе инструментальных панелей. Нужно будет выбрать панель Оборудование: Развертки и на панели выбрать тип объекта, развертку которого мы хотим получить.

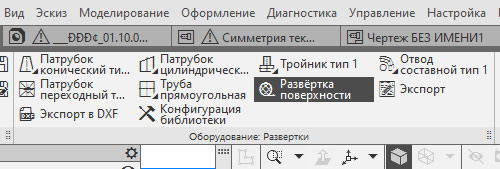
Построим развертку усеченного конуса, также как в первом примере. Выберем команду «Патрубок конический тип 1». На Панели параметров задаем данные по усеченному конусу: 2 диаметра и высоту и нажимаем «Создать объект»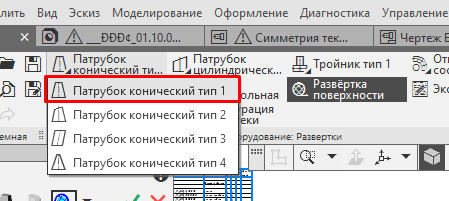

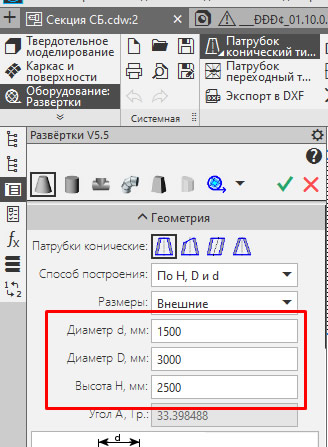
Откроется окно записи файла в котором нужно указать имя документа

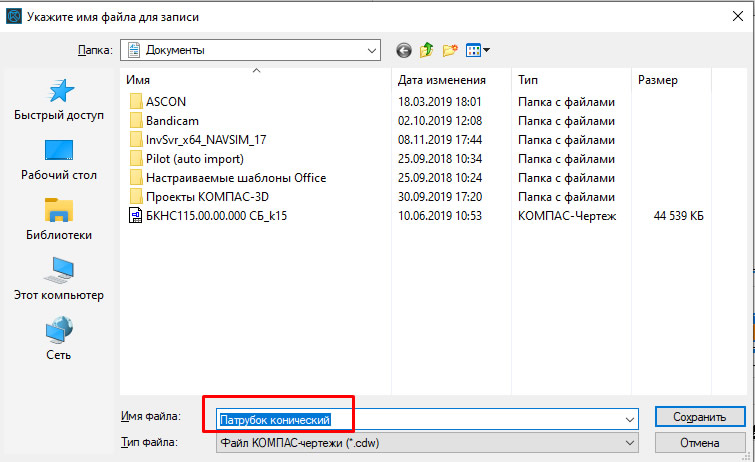
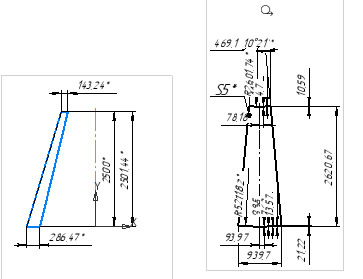
Получаем чертеж развертки с размерами:

Колпак на дымоход своими руками

Хозяева домов зачастую прибегают к использованию элементов в виде различных колпаков и зонтов, служащих, как это кажется на первый взгляд, для украшения дымовых труб. В то же время такие насадки не только улучшают эстетическое восприятие строения, но и обеспечивают полезную функциональность. Обычно так называемый козырек для дымохода изготавливается собственными силами, так как для этого не требуется серьезных знаний и умений. Хотя наряду с простой конструкцией этих элементов встречаются достаточно замысловатые поделки, которые проблематично соорудить без соответствующего опыта.

Конструктивные особенности

Колпак на дымоход представляет собой устройство, предназначенное для защиты трубы от попадания влаги. Внешний вид таких козырьков может быть различен, что имеет зависимость как от предпочтений хозяина дома, так и от конфигурации трубы.

Колпаки на трубу дымохода включают в себя:

• зонтик – устанавливаемая на вершине колпака защита от осадков, посторонних предметов и проникновения птиц, внешний вид которой имеет форму пирамиды, конуса или соответствует другой геометрии;
• фартук – часть колпака, отвечающая за защиту верха трубы от стекающей с зонтика воды. Обычно установка этого элемента производится при оснащении прямоугольной или квадратной трубы. В результате гарантируется увеличение срока службы дымохода, так как удается практически исключить вероятность появления коррозии и грибка;
• кронштейны – крепежные элементы, представляющие собой металлические полоски, которые позволяют соединить козырек и фартук. Непосредственное крепление в данном случае производится за счет использования сварки.

Имейте в виду! Собрать колпак для дымохода вполне реально самому, но только в том случае, если вы хотите установить достаточно простой флюгарок. Модели, отличающиеся большей сложностью в плане конструктивных особенностей, гораздо выгоднее заказать или купить.

При наличии выбора лучше всего отдать предпочтение тем моделям, которые оборудованы открывающейся крышкой. Это позволит проводить профилактический осмотр дымохода и его чистку без каких-либо проблем, что связано с комфортом доступа.

Колпак на дымоход долгого срока использования может быть изготовлен только из железа, устойчивого к коррозии: оцинкованная сталь, алюминий и медь. В последнем случае предлагаемый металл обладает ярко выраженным декоративным характером, так как его переливы на солнце могут придать вашем дому определенную респектабельность.

Одевают оголовок на трубу дымохода чтобы гасить искры. Это одно из его предназначений. Поэтому качество железа должно быть хорошим, тем самым оно долго не прогорит.

Виды

В связи с тем, что дымоходы отличаются разнообразием форм и размеров, производители колпаков также предлагают широкий ассортимент продукции. Если вы решите украсить свое жилище и продлить срок жизни дымохода, то придется выбирать среди большого ассортимента флюгарок:

1. Стандартные – зонт на дымоход в виде пирамидки, для изготовления которой используется листовой металл, а крепление к фартуку осуществляется посредством кронштейнов.
2. Четырехскатные – устанавливается преимущественно на прямоугольные трубы, выполненные из кирпича. По форме соотносится с вальмовой крышей с четырьмя скатами.
3. С полукруглым зонтиком – визуально отличается красотой, но обеспечивает недостаточную тягу. Преимущественно используется для установки на дымоходах домов, которые построены по европейским стандартам.
4. Плоские – часто можно встретить на зданиях в стиле модерн. Имеет прямоугольную форму и отличается таким недостатком, как повышенная нагрузка на кронштейны, что в некоторых случаях приводит к их деформации. Это связано с плоской крышей колпака, которая не дает возможность скатываться снегу. Данный факт определяет возникновение упомянутой проблемы.
5. Круглые с конусообразным зонтиком – модели без капельника, устанавливаемые на выполненные из нержавейки дымоходы круглого сечения.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.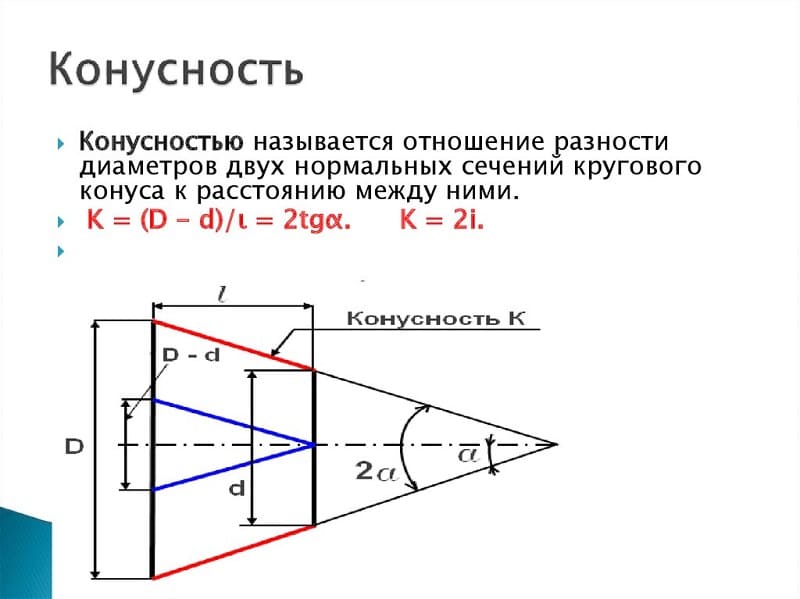

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Как определить уклон

Для определения уклона достаточно воспользоваться всего одной формулой. Как ранее было отмечено, существенно упростить задачу можно при построении прямоугольного треугольника. Среди особенностей подобной работы отметим следующие моменты:

1. Определяется начальная и конечная точка отрезка. В случае построения сложной фигуры она определяется в зависимости от особенностей самого чертежа.
2. Проводится вертикальная линия от точки, которая находится выше. Она позволяет построить прямоугольный треугольник, который часто используется для отображения уклона.
3. Под прямым углом проводится соединение вспомогательной линии с нижней точкой.
4. Угол, который образуется между вспомогательной и основной линией в нижней точке высчитывается для определения наклона.

Формула, которая требуется для вычисления рассматриваемого показателя указывалась выше. Стоит учитывать, что полученный показатель также переводится в градусы.

Задача на определение диаметра через известную площадь конуса и его образующую

Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?

Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:

r 2 + 14*r — 150/3,14 = 0

При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:

D = 14 2 — 4*1*(-150/3,14) = 387,0828

Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:

Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:

r = (-14+√387,0828)/2 = 2,837 см

Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.

В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.

Нормальные углы и конусы инструментов

НОРМАЛЬНЫЕ УГЛЫ ( ГОСТ 8908-81 )

&nbsp Таблица не распространяется на угловые размеры конусов. При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.

НОРМАЛЬНЫЕ КОНУСНОСТИ и УГЛЫ КОНУСОВ ( ГОСТ 8593-81 )

&nbsp Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.

&nbsp Примечание. Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.

КОНУСЫ ИНСТРУМЕНТОВ УКОРОЧЕННЫЕ ( ГОСТ 9953-82 )

&nbsp Стандарт распространяется на укороченные инструментальные конусы Морзе.

&nbsp *z — наибольшее допускаемое отклонение положения основной плоскости, в которой находится диаметр D от теоретическогот положения. &nbsp ** размеры для справок.

КОНУСНОСТЬ НАРУЖНЫХ И ВНУТРЕННИХ КОНУСОВ И КОНУСОВ С РЕЗЬБОВЫМ ОТВЕРСТИЕМ

РЕКОМЕНДУЕМЫЕ РАЗМЕРЫ ЦЕНТРОВОГО ОТВЕРСТИЯ УКОРОЧЕННОГО КОНУСА

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ НАРУЖНЫЕ( ГОСТ 25557-2006 )

&nbsp Профиль резьбового отверстия соответствует отверстию центровому форма Р по ГОСТ ГОСТ 14034-74.

&nbsp В ГОСТ 25557-2006 все размеры центрового отверстия приводятся в общей таблице. Стандарт также определяет размеры пазов канавок и отвестий, необходимых для конструирования конусов, в случае подачи смазочно-охлаждающей жидкости (СОЖ) через инструмент.

&nbsp В зависимости от конструкции инструментальный хвостовик может иметь соответствующее обозначение:

BI — внутренний конус с пазом; BE — наружный конус с лапкой; AI — внутренний конус с отверстием по оси; АЕ — наружный конус с резьбовым отверстием по оси; BIK — внутренний конус с пазом и отверстием для подачи СОЖ; ВЕК — наружный конус с лапкой и отверстием для подачи СОЖ; AIK — внутренний конус с отверстием по оси и отверстием для подачи СОЖ; АЕК — наружный конус с резьбовым отверстием по оси и отверстием для подачи СОЖ.

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ ВНУТРЕННИЕ( ГОСТ 25557-2006 )

КОНУСЫ ВНУТРЕННИЕ И НАРУЖНЫЕ КОНУСНОСТЬЮ 7 : 24 ( ГОСТ 15945-82 )

&nbsp Допуски конусов внутренних и наружных конусностью 7:24 по ГОСТ 19860-93.

КОНУСЫ ИНСТРУМЕНТОВ Предельные отклонения угла конуса и допуски формы конусов ( ГОСТ 2848-75 )

&nbsp Степень точности инструментальных конусов обозначается допуском угла конуса заданной степени точности по ГОСТ 8908-81 и определяется предельными отклонениями угла конуса и допусками формы поверхности конуса, числовые значения которых указаны ниже.

&nbsp Примечания: &nbsp 1. Отклонения угла конуса от номинального размера располагав в «плюс» — для наружных конусов, в «минус» — для внутренних. &nbsp 2. ГОСТ 2848-75 для наружных конусов предусматривает также степени точности АТ4 и АТ5. Допуски по ГОСТ 2848-75 распространяются на конусы инструментов по ГОСТ 25557-2006 и ГОСТ 9953-82.

&nbsp Пример обозначения конуса Морзе 3, степени точности АТ8:

Морзе 3 АТ8 ГОСТ 25557-2006

&nbsp То же метрического конуса 160, степени точности АТ7:

Метр. 160 АТ7 ГОСТ 25557-2006

&nbsp То же укороченного конуса В18, степени точности АТ6:

Морзе В18 АТ6 ГОСТ 9953-82

ГОСТ 2848-75 — Конусы инструментов. Допуски. Методы и средства контроля ГОСТ 7343-72 — Конусы инструментов с конусностью 1:10 и 1:7. Размеры ГОСТ 10079-71 — Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры ГОСТ 22774-77 — Конусы и трубки шлифовальные. Типы и размеры ГОСТ 25548-82 — Основные нормы взаимозаменяемости. Конусы и конические соединения. Термины и определения

Объем конуса, его расчет

Геометрия как наука сформировалась в Древнем Египте и достигла высокого уровня развития

Известный философ Платон основал Академию, где пристальное внимание уделялось систематизации имеющихся знаний. Конус как одна из геометрических фигур впервые упоминается в известном трактате Евклида «Начала»

Евклид был знаком с трудами Платона. Сейчас мало кто знает, что слово «конус» в переводе с греческого языка обозначает «сосновая шишка». Греческий математик Евклид, живший в Александрии, по праву считается основоположником геометрической алгебры. Древние греки не только стали преемниками знаний египтян, но и значительно расширили теорию.

Вы здесь

ОБРАБОТКА КОНИЧЕСКИХ ПОВЕРХНОСТЕЙ

§ 1. Общие сведения 1. Область применения конусов. Наряду с цилиндрическими деталями в машиностроении получили довольно широкое распространение детали с коническими поверхностями. Примерами их могут служить конусы центров, хвостовиков сверл, зенкеров, разверток. Для крепления этих инструментов передние участки отверстий шпинделя и пиноли токарного станка имеют также коническую форму. Однако область использования конусов не ограничивается режущими инструментами. Конические поверхности имеют многие детали машин. Широкое использование конических соединений объясняется рядом их преимуществ. 1. Они обеспечивают высокую точность центрирования деталей. 2. При плотном соприкосновении пологих конусов получается неподвижное соединение. 3. Изменяя осевое положение деталей конического соединения, можно регулировать величину зазора между ними. 2. Конус и его элементы. Конус представляет собой геометрическое тело, поверхность которого получается вращением прямой линии (образующей), наклонно расположенной к оси вращения (рис. 129, а). Точка пересечения образующей с осью называется вершиной конуса. Плоскости, перпендикулярные к оси конуса, называются, основаниями. Различают полный и усеченный конусы. Первый расположен между основанием и вершиной, второй — между двумя основаниями (большим и меньшим). Конус характеризуется следующими элементами: диаметром большего основания D; диаметром меньшего основания d; длиной l; углом уклона а между образующей и осью конуса; углом конуса 2а между противоположными образующими. Кроме этого, на рабочих чертежах конических деталей часто употребляют понятия конусность и уклон. Конусностью называется отношение разности диаметров двух перечных сечений конуса к расстоянию между ними. Она опреляется по формуле Уклоном называется отношение разности радиусов двух поперечных сечений конуса к расстоянию между ними. Его определяют по формуле Из формул (9) и (10) видно, что уклон равен половине конусности. Тригонометрически уклон равен тангенсу угла уклона (см. рис. 129, б, треугольник ABC), т. е. На чертеже (рис. 130) конусность обозначают знаком <, а уклон —, острие которых направляется в сторону вершины конуса. После знака указывается отношение двух цифр. Первая из них соответствует разности диаметров в двух принятых сечениях конуса, вторая для конусности— расстояние между сечениями, для уклона — удвоенной величине этого расстояния. Конусность и уклон иногда записываются числами десятичной дроби: 6,02; 0,04; 0,1 и т. д. Для конусности эти цифры соответствуют разности диаметров конуса на длине 1 мм, для уклона — разности радиусов на этой же длине. Для обработки полного конуса достаточно знать два элемента: диаметр основания и длину; для усеченного конуса — три элемента: диаметры большего и меньшего оснований и длину. Вместо одного из указанных элементов может быть задан угол наклона а, уклон или конусность. В этом случае для определения недостающих размеров пользуются вышеприведенными формулами (9), (10) и (11). Пример 1. Дан конус, у которого d=30 мм, /=500 мм, К=1: 20. Определить больший диаметр конуса. Решение. Из формулы (9) Пример 2. Дан конус, у которого D=40 мм, l = 100 мм, а=5 , Определить меньший диаметр конуса. Решение. Из формулы (11) По таблице тангенсов находим tg5°=0,087. Следовательно, d=40—2*100Х Х0,87=22,6 мм. Пример 3. Определить угол уклона а, если на чертеже указаны размеры конуса: D—50 мм, d=30 мм, /=200 мм. Решение. По формуле (11) Из таблицы тангенсов находим а=2 50 . Пример 4. Дан конус, у которого D=60 мм, /=150 мм, К=1 : 50. Определить угол уклона а. Решение. Так как уклон равен половине конусности, можно записать: По таблице тангенсов находим а=0 30 . 3. Нормальные конусы. Конусы, размеры которых стандартизованы, называются нормальными. К ним относятся конусы Морзе, метрические, конусы для насадных разверток и зенкеров с конусностью 1:50 0, под конические штифты — с конусностью 1:50, для конических резьб с конусностью 1 : 16 и др. Наибольшее распространение в машиностроении получили инструментальные конусы Морзе и метрические, основные размеры которых приведены в табл. 13.

Размеры конусов Морзе выражаются дробными числами. Это объясняется тем, что впервые стандарт на них был принят в дюймовой системе измерения, которая сохранилась до настоящего времени. Конусы Морзе имеют различную конусность (примерно 1 20), метрические конусы одинаковую — 1:20. Автор — nastia19071991

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

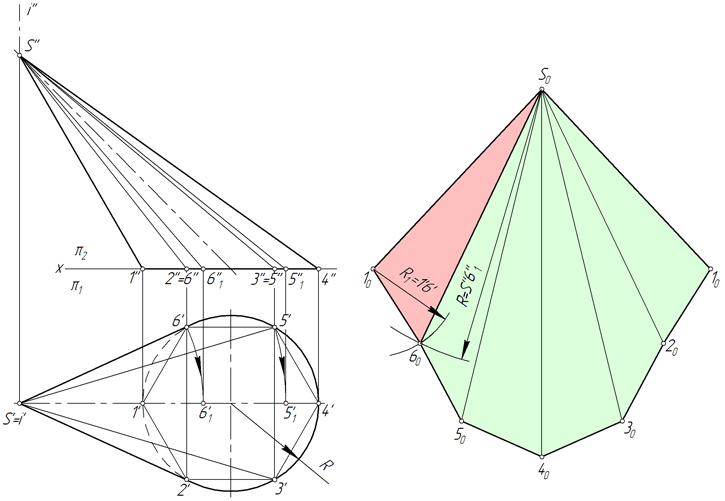
1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S. Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’₁, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

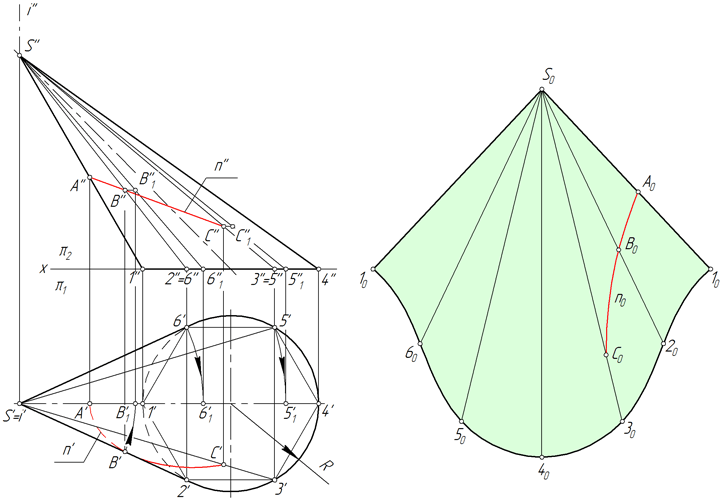
1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
3. Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
4. Соединяем точки A, B, C плавной линией.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ Р 50017-92 (ИСО 575-78) Машины текстильные и оборудование вспомогательное. Патроны конические переходные. Половина угла конуса 4°20′. Размеры и методы контроля

ГОСТ Р 50018-92 (ИСО 324-78) Машины текстильные и оборудование вспомогательное. Патроны конические для крестовой намотки при крашении (крестовая намотка). Половина угла конуса 4°20′. Размеры и методы контроля

ГОСТ Р 50042-92 (ИСО 368-82) Машины текстильные и оборудование вспомогательное. Патроны для веретен кольцепрядильных и крутильных машин. Конус 1:38 и 1:64. Размеры

ГОСТ Р 50213-92 (ИСО 5237-78) Машины текстильные и оборудование вспомогательное. Патроны конические для намотки пряжи (крестовая намотка). Половина угла конуса 5°57′. Размеры и методы контроля

ГОСТ Р 50663-99 (ИСО 8382-88) Аппараты искусственной вентиляции легких для оживления. Общие технические требования и методы испытаний

ГОСТ 2.320-82 Единая система конструкторской документации. Правила нанесения размеров, допусков и посадок конусов

ГОСТ 8032-84 Предпочтительные числа и ряды предпочтительных чисел

ГОСТ 15945-82 Конусы внутренние и наружные конусностью 7:24. Размеры

ГОСТ 22967-90 Шприцы медицинские инъекционные многократного применения. Общие технические требования и методы испытаний

ГОСТ 24264-93 (ИСО 5356-1-87) Аппараты ингаляционного наркоза и искусственной вентиляции легких. Соединения конические. Часть 1. Конические патрубки и гнезда

ГОСТ 25557-2006 (ИСО 296-91) Конусы инструментальные. Основные размеры

Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.

Уклон и Конусность

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.

Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали.

Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона.

Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах

Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах.

Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.

Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.