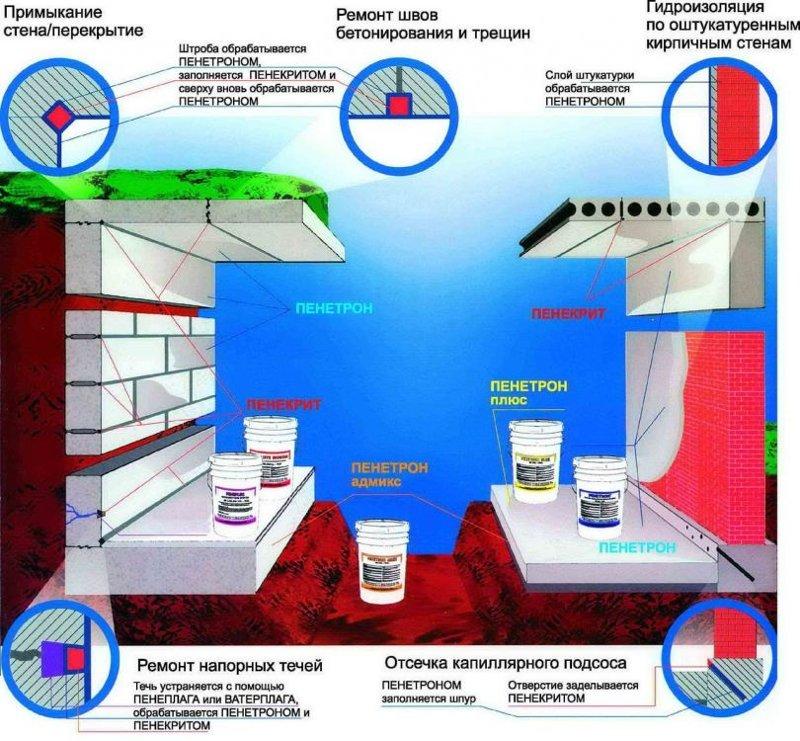
Модуль упругости бетона: виды, классификация. от чего зависит. модуль упругости железобетона

Модуль упругости бетона в20

• Классификация
  • Виды и таблицы
  • Модуль упругости — от чего он зависит
• Заключение

Все растворы склонные к затвердеванию обладают определённой плотностью в застывшем состоянии, поэтому и существует такое понятие, как модуль упругости бетона, по которому и определяется его пригодность к тому или иному виду работ. Помимо этого такие смеси классифицируются еще и по маркам, но марка может включать размеров плотности и имеет более общее понятие.

Именно об этом пойдёт речь ниже, а также вы сможете увидеть здесь демонстрацию тематического видео в этой статье.

Испытание на растяжение

Виды и таблицы

Заливка плитного фундамента

• Все виды подобных растворов подразделяются на тяжёлые, мелкозернистые, лёгкие, поризованные, а также автоклавного твердения. Вызывает некоторое удивление, что чуть ли не все доморощенные строители об этом не имеют почти никаких знаний, хотя от этого в основном зависит качество возводимой конструкции.
• Сами по себе бетонные изделия являются достаточно твёрдыми материалами, но под воздействием механических нагрузок типа удара, сжатия растяжения и излома даже самый высокий модуль упругости железобетона не может быть вполне достаточным, как абсолютная единица. В связи с этим классификация прочности различается на два основных показателя — сжатие и растяжение, от которых зависит переносимость других нагрузок или упругость.

Наименование бетона	Модуль упругости начальный. Сжатие и растяжение Eb*103. Прочность на сжатие в МПа
B1	B1,5	B2	B2,5	B3,5	B5	B7,5	B10	B12,5	В15	В20	В25	В30	B35	B40	B45	B50	B55	B60
Тяжёлые
Естественный цикл затвердевания	—	—	—	9,5	13	16	18	21	23	27	30	32,5	34,5	36	37,5	39	39,5	40
Тепловая обработка при атмосферном давлении	—	—	—	—	8,5	11,5	14,5	16	19	20,5	24	27	29	31	32,5	34	35	35,5	36
Автоклавная обработка	—	—	—	—	7	10	12	13,5	16	17	20	22,5	24,5	26	27	28	29	29,5	30
Мелкозернистые
А-группа (естественное отвердение)	—	—	—	—	7	10	13,5	15,5	17,5	19,5	22	24	26	27,5	28,5	—	—	—	—
Тепловая обработка при атмосферном давлении	—	—	—	—	6,5	9	12,5	14	15,5	17	20	21,5	23	24	24,5	—	—	—	—
Б-группа (естественное отвердение)	—	—	—	—	6,5	9	12,5	14	15,5	17	20	21,5	23	—	—	—	—	—	—
Теплообработка при автоклавном давлении	—	—	—	—	5,5	8	11,5	13	14,5	15,5	17,5	19	20,5
В-группа автоклавного отвердения	—	—	—	—	—	—	—	—	—	16,5	18	19,5	21	21	22	23	24	24,5	25
Лёгкие и горизонтальные — средняя плотность D
800	—	—	—	4	4,5	5	5,5	—	—	—	—	—	—	—	—	—	—	—	—
1000	—	—	—	5	5,5	6,3	7,2	8	8,4	—	—	—	—	—	—	—	—	—	—
1200	—	—	—	6	6,7	7,6	8,7	9,5	10	10,5	—	—	—	—	—	—	—	—	—
1400	—	—	—	7	7,8	8,8	10	11	11,7	12,5	13,5	14,5	15,5	—	—	—	—	—	—
1600	—	—	—	—	9	10	11,5	12,5	13,2	14	15,5	16,5	17,5	18	—	—	—	—	—
1800	—	—	—	—	—	11,2	13	14	14,7	15,5	17	18,5	19,5	20,5	21	—	—	—	—
2000	—	—	—	—	—	—	14,5	16	17	18	19,5	21	22	23	23,5	—	—	—	—
Ячеистые, автоклавное твердение, плотность D
500	1,1	1,4	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—
600	1,4	1,7	1,8	2,1	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—
700	—	1,9	2,2	2,5	2,9	—	—	—	—	—	—	—	—	—	—	—	—	—	—
800	—	—	—	2,9	3,4	4	—	—	—	—	—	—	—	—	—	—	—	—	—
900	—	—	—	—	3,8	4,5	5,5	—	—	—	—	—	—	—	—	—	—	—	—
1000	—	—	—	—	—	6	7	—	—	—	—	—	—	—	—	—	—	—	—
1100	—	—	—	—	—	6,8	7,9	8,3	8,6	—	—	—	—	—	—	—	—	—	—
1200	—	—	—	—	—	—	8,4	8,8	9,3	—	—	—	—	—	—	—	—	—	—

Таблица модулей упругости бетона с учётом СНИП 2.03.01-84

Примечание. Не забывайте о том, что при нагрузке конструкции не подвергаются необратимым процессам, вызывающим критические разрушения — их свойства не изменяются. Это следует учитывать при сооружении арок или перекрытий.

Рекомендация

При монтаже тех или иных конструкций всегда следует обращать внимание на таблицы, как того требует инструкция

Модуль упругости — от чего он зависит

Бетонные арки. Фото

В первую очередь, упругость зависит от характеристик наполнителя, к тому же, если отобразить такое влияние на графической схеме, то мы увидим прямолинейное возрастание.

Получается, что чем выше значение модуля, тем больше упругость раствора, где самые высокие показатели у тяжёлых бетонов, так как там используются очень плотные наполнители — щебень и гравий.

Также, на упругость влияет время заливки конструкции или её возраст, но показатели меняются в зависимости от первоначального модуля.

Но в среднем можно сказать, что бетон постоянно набирает крепость примерно в течение 50 лет! Примечательно, что все эти показатели не изменяются под воздействием температуры до 230⁰C, следовательно, вред бетону может быть нанесён только очень сильным пожаром.

Автоклавная обработка

Влияет на показатели процесс затвердевания раствора, который может происходить при термической обработке открытым способом, через автоклав или естественным образом.

Для определения продолжительности возможной нагрузки вы берёте начальный модуль (из таблицы) и умножаете его на коэффициент, который равен 0,85.

для лёгких, мелкозернистых и тяжёлых бетонов и 0,7 для  поризованных.

Приготовление бетона своими руками при строительстве дома

Что такое расчетное сопротивление?

Расчетное сопротивление бетонной смеси – характеристика отражающая свойство материала противостоять внешним механическим нагрузкам. Его применяют при проектировании зданий и сооружений. Данный показатель получают из нормативных значений противодействия конкретной марки раствора делением на специальный коэффициент.

Этот коэффициент, применяемый для вычисления расчетного сопротивления бетона на сжатие обозначается γb и может принимать значения:

• 1,3 – для максимальных возможных величин по несущей способности;
• 1 – для максимальных значений по пригодности к эксплуатации.

Коэффициенты надежности материала при механическом растяжении обозначаются γbt, они могут быть равны:

• 1,5 – для максимальных показателей несущей способности во время определения класса на сжатие;
• 1,3 – для максимальных значений несущей способности на осевое растяжение;
• 1 – для максимальных величин по пригодности к эксплуатации.

Классы бетонов обозначаются от В10 до В60, значения их нормативного противодействия приводятся в специальных таблицах.

Как получить расчетное сопротивление?

Для получения расчетного сопротивления бетона по осевому сжатию определяется класс материала, из таблицы берутся его нормативные данные и производится вычисление по формуле:

Rb=Rbn/γb,

где Rb – расчетные данные на осевое сжатие, множитель Rbn – нормативные , γb – коэффициент.

Аналогично рассчитывают расчетное сопротивление бетона осевому растяжению:

Rbt=Rbtn/γbt,

где Rbt – расчетные значения на осевое растяжение, множитель Rbtn – нормативные показатели на растяжение, γbt – коэффициент для растяжения.

Учитывая условия, в которых будут эксплуатироваться бетонные конструкции, вводятся и другие коэффициенты γbi, учитывающие эти особенности:

• для непродолжительных статических нагрузок 1;
• для длительных статических нагрузок 0,9;
• элементы, заливаемые вертикально 0,9;
• коэффициенты, отражающие климатические особенности, назначение сооружения, площадь сечения указываются в документации отдельно.

Модуль деформаций бетона

Начальный модуль упругости бетона при сжатии соответствует лишь упругим деформациям, возникающим при мгновенном загружении или при напряжениях . Он определяется в соот­ветствии с законом Гука как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 1.11), т.е.

где р = 1 МПа — масштабно-размерный коэффициент.

Обычно определяется из специальных опытов на призмах при низком уровне напряжений (), когда бетон можно рассматривать как упругий материал.

При действии на бетон нагрузки, при которой , хотя бы в течение нескольких минут, в связи с развитием пластических деформаций (включая ползучесть) модуль полных деформаций бе­тона становится величиной переменной.

Для расчёта железобетонных конструкций пользуются сред­ним модулем деформаций или модулем упругопластичности бетона, представляющим собой тангенс угла наклона секущей, проведённой через начало координат и точку на кривой с заданным на­пряжением, к оси абсцисс, т.е.

Начальный модуль упругости бетона при растяжении по аб­солютной величине принимается равным , то есть , а

где vt = 0,15 — значение коэффициента упругопластичности бетона при растяжении в момент, предшествующий разрушению.

Значения модуля сдвига бетона G принимают по установленной в теории упругости зависимости

Подставив в неё начальный коэффициент поперечной деформации бетона ν=0,2, получим .

ЛЕКЦИЯ 3

Арматура для железобетонных конструкций

1. Назначение арматуры и требования к ней

2. Виды арматуры

3. Физико-механические свойства арматурных сталей

4. Классификация арматуры по основным характери­стикам. Сортамент арматуры

5. Сварные арматурные изделия

6. Соединения арматуры

1. Назначение арматуры и требования к ней

Под арматурой понимают отдельные стержни или целые каркасы, которые располагаются в массе бетона в соответствии со статиче­ской схемой работы конструкции.

Арматура в железобетонных конструкциях используется пре­имущественно для восприятия растягивающих усилий. Но иногда арматуру применяют и для усиления сжатого бетона (например, в колоннах), а также для восприятия температурных и усадочных на­пряжений.

Арматура для железобетонных конструкций должна удовлетво­рять следующим требованиям:

под нагрузкой надёжно работать совместно с бетоном (за счёт сцепления) на всех стадиях службы конструкции;

использоваться до предела текучести или предела прочности при исчерпании конструкцией несущей способности.

2. Виды арматуры

Многообразие видов железобетонных конструкций определяет необ­ходимость применения широкой номенклатуры арматурных сталей.

Для изготовления арматуры используют конструкционные стали обычно с содержанием углерода не более 0,65%, так как стали с более высоким содержанием углерода плохо свариваются.

Арматура классифицируется по функциональному назначению и способу изготовления по четырём признакам.

1. По технологии изготовления арматуру делят на: стержневую го­рячекатаную, термомеханически упрочненную и механически упрочненную в холодном состоянии (холоднодеформированную).

2. По форме наружной поверхности арматура бывает гладкая и пе­риодического профиля.

3. По способу применения: арматура, которую укладывают в кон­струкцию без предварительного напряжения, называется ненапрягаемой, арматура, которую при изготовлении конструкции предва­рительно натягивают — напрягаемой.

4. Арматура, устанавливаемая в железобетонных конструкциях по расчёту, называется рабочей. Площадь её поперечного сечения опре­деляется расчётом элементов конструкций на различные нагрузки и воздействия. Её главное назначение — восприятие растягивающих усилий в сечениях. Поэтому она располагается в растянутой зоне вдоль линии действия этих усилий, т. е. перпендикулярно к воз­можному направлению трещин.

Арматура, устанавливаемая по конструктивным или технологи­ческим соображениям, называется монтажной или распределитель­ной (в плитах). Она обеспечивает проектное положение рабочей ар­матуры в конструкции и более равномерно распределяет усилия между отдельными стержнями рабочей арматуры. Кроме того, мон­тажная арматура может воспринимать обычно не учитываемые рас­чётом усилия от усадки бетона, изменения температуры конструк­ции и т. п. Она может также выполнять роль рабочей при транспор­тировании и монтаже конструкции.

Детальное определение

Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях.

Пусть l и d длина и поперечный размер образца до деформации, а l ′ > и d ′ > — длина и поперечный размер образца после деформации. Тогда продольным удлинением

называют величину, равную ( l ′ − l ) -l)> , а поперечнымсжатием — величину, равную − ( d ′ − d ) -d)> . Если ( l ′ − l ) -l)> обозначить как Δ l , а ( d ′ − d ) -d)> как Δ d , тоотносительное продольное удлинение будет равно величине Δ l l >> , аотносительное поперечное сжатие — величине − Δ d d >> . Тогда в принятых обозначениях коэффициент Пуассона μ имеет вид:

μ = − Δ d d l Δ l . >>.>

Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся 0>»> Δ l l > 0 >>0> 0>»/> и Δ d d 0 > , так что коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении.

Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он равен приблизительно 0,5.

Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается.

К примеру, бумага из одно

слойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения долимного слойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20.

Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы , так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0,54), натрий (−0,44), калий (−0,42), кальций (−0,27), медь (−0,13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона.

ДЕФОРМАЦИИ БЕТОНА ПРИ КРАТКОВРЕМЕННОМ НАГРУЖЕНИИ. МОДУЛЬ УПРУГОСТИ БЕТОНА

ВЫСОКОПРОЧНЫЙ БЕТОН

Бетон как материал, не подчиняющийся закону Гука, имеет диаграмму сжатия криволинейного очертания. Из­вестны различные варианты математического описания кривой G = /(є), в основу которых положены эксперимен­тальные закономерности . Исследования, зна­чительная часть которых была проведена в ЦНИИС , позволили связать характерную форму этой кривой с физическими процессами деформирования и раз­рушения бетона (см. главу II).

При кратковременном возрастании статической на­грузки отклонение диаграммы сжатия от прямолинейной обусловлено преимущественно нарушением сплошности ма­териала, вследствие перехода границы микроразрушения Rr по мере роста нагрузки и дальнейшим развитием микро­трещин в бетоне . В более общем случае степень искривления диаграммы зависит также от скорости нагру­жения, поскольку наблюдаемые деформации включают опре­деленную долю деформаций ползучести, проявляющихся ча­стично на всех уровнях нагрузки. Поэтому даже при не­больших нагрузках (в зоне так называемой линейной ползучести) обнаруживается некоторая криволинейность диаграммы . Вследствие этого модуль деформаций бетона, определяемый как тангенс угла наклона секущей к кривой о — є, не является постоянной величиной и умень­шается по мере роста напряжений.

Для практических оценок пределов изменения секущего модуля под кратковременной нагрузкой необходимо рас­полагать данными, по крайней мере, о двух параметрах кривой а — є, начальном угле наклона этой кривой (на­чальный модуль деформаций) и величине деформаций, соответствующей максимуму кривой (предельная деформа­ция под кратковременной нагрузкой). В указанном диапа­зоне модуль деформаций изменяется более или менее плавно . Значения обоих параметров, а также характер изменения модуля деформаций с ростом напряжений от нуля до максимальной величины существенно зависят от особенностей структуры бетона .

Рассмотрим характеристики деформативной способности бетона при кратковременном нагружении (начальный мо­дуль деформаций и величину предельной деформативности), которые наиболее часто применяются для расчетов эле­ментов конструкций.

Хотя наибольшее число экспериментальных данных в этой области получено при испытании бетонов в условиях одноосного сжатия, установленные закономерности можно с достаточным основанием использовать применительно к действию растягивающих напряжений в бетоне .

В лабораторных условиях начальный модуль дефор­маций бетона Е = ^ находят при определенной величине

Относительного уровня напряжений в бетоне, составляющей 20—30% предела прочности опытных образцов . В этой области напряжений (и вплоть до границы R?) кривая, характеризующаяся зависимостью а — є, имеет незначи­тельную кривизну, поэтому начальный модуль деформаций практически не зависит от величины напряжений. Пов­торным нагружением бетона в зоне невысоких напряжений до некоторой степени можно исключить влияние остаточных деформаций бетона на величину модуля. Определенную таким путем характеристику деформативности бетона с не­нарушенной структурой рассматривают условно как модуль упругости (начальный модуль упругости) этого материала.

Кольца колодцев

Кольца колодцев были и остаются очень востребованным строительным материалом. К слову, кольца колодцев приобретают не только те, чья деятельность связана с водоснабжением и канализацией, но и телефонисты, Интернет-провайдеры и, конечно …

ОСОБЕННОСТИ ВЗАИМОСВЯЗИ МОДУЛЯ УПРУГОСТИ И ПРОЧНОСТИ БЕТОНА

Полученное выражение (V.15) дает возможность сфор­мулировать общее положение о характере зависимости меж — ду упругими и прочностными свойствами тяжелого бето­на. Особенность этой связи заключается в том, что оца не является …

ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЕЛИЧИНУ УСАДКИ БЕТОНА

Об усадке тяжелого бетона имеется не меньше экспе­риментальных данных, чем о его ползучести. Попытки- использовать эти данные для получения общих количест­венных закономерностей явления содержатся в ряде работ. При оценке возможной …

Влияние температуры на изменение механических свойств материалов

Твердое состояние — не единственное агрегатное состояние вещества. Твердые тела существуют только в определенном интервале температур и давлений. Повышение температуры приводит к фазовому переходу из твердого состояния в жидкое, а сам процесс перехода называется плавлением. Температуры плавления, как и другие физические характеристики материалов, зависят от множества факторов и также определяются опытным путем.

Таблица 318.6. Температуры плавления некоторых веществ

Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).

Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20оС. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35оС.

При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σп, σт и σв) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.

Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.

При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σв1100 = 2σв20.

Характеристики пластичности меди, медных сплавов и магния с ростом температуры уменьшаются, а алюминия — увеличиваются. При нагреве пластмасс и резины их предел прочности резко снижается, а при охлаждении эти материалы становятся очень хрупкими.

Способы определения модуля упругости

Ультразвуковой способ контроля модуля упругости бетона.

Норматив упругости конструкции выясняется в ходе экспериментальных исследований на пробах по бетону Данное значение принято обозначать буквой «Е». Однако у него имеется и другое обозначение – «модуль Юнга». Профессионалы разделяют показатель упругости на подвиды: начальный и приведенный.

Необходимо заметить, что обычному малоопытному потребителю непростые формулы и примеры вычетов, которые делаются по данному показателю, никоим образом не пригодятся в жизни. В подобных тонкостях и нюансах может разобраться лишь человек опытный либо владеющий специальным образованием.

Показатель упругости возможно выяснить во время проведения отдельных проб на способность противостоять сжатию либо растяжению. Стоит заметить, что материал, не содержащий внутри армировочный каркас к такому явлению как растяжение, не подвластен. По результатам проведенных экспериментов, происходит построение графика, в котором указана зависимость между прикладываемым воздействием и разрушением изделия.

Начальный показатель, характеризующийся упругостью бетона, выясняется не так легко, как хотелось бы. Но его примерное значение можно выяснить косвенным методом. Довольно часто секущая полоса к кривой, обозначающая зависимость воздействия от разрушения, расположена параллельно относительно касательной линии. Также правильным будет определение того, что показатель упругости материала повышается прямо пропорционально значению его крепости. Но все-таки это является точным лишь для главной части графика. Также значение сильно подвластно условиям и месту эксперимента.

Способы определения и контроля показателей прочности металлов

Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.

Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними.

Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда.

С повышением прочностных характеристик совершенствовались инструменты и способы производства.

Виды нагрузок

При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.

Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.

Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.

Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.

Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.

Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.

В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:

1. Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
2. Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).

Формула по закону Гука записывается в виде ε = σz/E, где:

• ε – относительное удлинение;
• σz – нормальное напряжение.

Демонстрация закона Гука для упругих тел:

Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.

Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.

В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.

Значения модуля упругости для некоторых материалов приведены в таблице 1.

Таблица 1: Модуль упругости для металлов и сплавов

Наименование материала	Значение модуля упругости, 10¹²·Па
Алюминий	65…72
Дюралюминий	69…76
Железо, содержание углерода менее 0,08 %	165…186
Латунь	88…99
Медь (Cu, 99 %)	107…110
Никель	200…210
Олово	32…38
Свинец	14…19
Серебро	78…84
Серый чугун	110…130
Сталь	190…210
Стекло	65…72
Титан	112…120
Хром	300…310

Понятие о модуле упругости

В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:

1. Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
2. Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).

алюминий, медь, стекло, железо и многое другое.

Материал	Коэффициент линейного теплового расширения
(10-6 м/(мK)) / ( 10-6 м/(мoС))	(10-6 дюйм/(дюйм oF))
ABS (акрилонитрил-бутадиен-стирол) термопласт	73.8	41
ABS — стекло, армированное волокнами	30.4	17
Акриловый материал, прессованный	234	130
Алмаз	1.1	0.6
Алмаз технический	1.2	0.67
Алюминий	22.2	12.3
Ацеталь	106.5	59.2
Ацеталь , армированный стекловолокном	39.4	22
Ацетат целлюлозы (CA)	130	72.2
Ацетат бутират целлюлозы (CAB)	25.2	14
Барий	20.6	11.4
Бериллий	11.5	6.4
Бериллиево-медный сплав (Cu 75, Be 25)	16.7	9.3
Бетон	14.5	8.0
Бетонные структуры	9.8	5.5
Бронза	18.0	10.0
Ванадий	8	4.5
Висмут	13	7.3
Вольфрам	4.3	2.4
Гадолиний	9	5
Гафний	5.9	3.3
Германий	6.1	3.4
Гольмий	11.2	6.2
Гранит	7.9	4.4
Графит, чистый	7.9	4.4
Диспрозий	9.9	5.5
Древесина, пихта, ель	3.7	2.1
Древесина дуба, параллельно волокнам	4.9	2.7
Древесина дуба , перпендикулярно волокнам	5.4	3.0
Древесина, сосна	5	2.8
Европий	35	19.4
Железо, чистое	12.0	6.7
Железо, литое	10.4	5.9
Железо, кованое	11.3	6.3
Золото	14.2	8.2
Известняк	8	4.4
Инвар (сплав железа с никелем)	1.5	0.8
Инконель (сплав)	12.6	7.0
Иридий	6.4	3.6
Иттербий	26.3	14.6
Иттрий	10.6	5.9
Кадмий	30	16.8
Калий	83	46.1 — 46.4
Кальций	22.3	12.4
Каменная кладка	4.7 — 9.0	2.6 — 5.0
Каучук, твердый	77	42.8
Кварц	0.77 — 1.4	0.43 — 0.79
Керамическая плитка (черепица)	5.9	3.3
Кирпич	5.5	3.1
Кобальт	12	6.7
Констанан (сплав)	18.8	10.4
Корунд, спеченный	6.5	3.6
Кремний	5.1	2.8
Лантан	12.1	6.7
Латунь	18.7	10.4
Лед	51	28.3
Литий	46	25.6
Литая стальная решетка	10.8	6.0
Лютеций	9.9	5.5
Литой лист из акрилового пластика	81	45
Магний	25	14
Марганец	22	12.3
Медноникелевый сплав 30%	16.2	9
Медь	16.6	9.3
Молибден	5	2.8
Монель-металл (никелево-медный сплав)	13.5	7.5
Мрамор	5.5 — 14.1	3.1 — 7.9
Мыльный камень (стеатит)	8.5	4.7
Мышьяк	4.7	2.6
Натрий	70	39.1
Нейлон, универсальный	72	40
Нейлон, Тип 11 (Type 11)	100	55.6
Нейлон, Тип 12 (Type 12)	80.5	44.7
Нейлон литой , Тип 6 (Type 6)	85	47.2
Нейлон, Тип 6/6 (Type 6/6), формовочный состав	80	44.4
Неодим	9.6	5.3
Никель	13.0	7.2
Ниобий (Columbium)	7	3.9
Нитрат целлюлозы (CN)	100	55.6
Окись алюминия	5.4	3.0
Олово	23.4	13.0
Осмий	5	2.8
Палладий	11.8	6.6
Песчаник	11.6	6.5
Платина	9.0	5.0
Плутоний	54	30.2
Полиалломер	91.5	50.8
Полиамид (PA)	110	61.1
Поливинилхлорид (PVC)	50.4	28
Поливинилденфторид (PVDF)	127.8	71
Поликарбонат (PC)	70.2	39
Поликарбонат — армированный стекловолокном	21.5	12
Полипропилен — армированный стекловолокном	32	18
Полистирол (PS)	70	38.9
Полисульфон (PSO)	55.8	31
Полиуретан (PUR), жесткий	57.6	32
Полифенилен — армированный стекловолокном	35.8	20
Полифенилен (PP), ненасыщенный	90.5	50.3
Полиэстер	123.5	69
Полиэстер, армированный стекловолокном	25	14
Полиэтилен (PE)	200	111
Полиэтилен — терефталий (PET)	59.4	33
Празеодимий	6.7	3.7
Припой 50 — 50	24.0	13.4
Прометий	11	6.1
Рений	6.7	3.7
Родий	8	4.5
Рутений	9.1	5.1
Самарий	12.7	7.1
Свинец	28.0	15.1
Свинцово-оловянный сплав	11.6	6.5
Селен	3.8	2.1
Серебро	19.5	10.7
Скандий	10.2	5.7
Слюда	3	1.7
Сплав твердый (Hard alloy) K20	6	3.3
Сплав хастелой (Hastelloy) C	11.3	6.3
Сталь	13.0	7.3
Сталь нержавеющая аустенитная (304)	17.3	9.6
Сталь нержавеющая аустенитная (310)	14.4	8.0
Сталь нержавеющая аустенитная (316)	16.0	8.9
Сталь нержавеющая ферритная (410)	9.9	5.5
Стекло витринное (зеркальное, листовое)	9.0	5.0
Стекло пирекс, пирекс	4.0	2.2
Стекло тугоплавкое	5.9	3.3
Строительный (известковый) раствор	7.3 — 13.5	4.1-7.5
Стронций	22.5	12.5
Сурьма	10.4	5.8
Таллий	29.9	16.6
Тантал	6.5	3.6
Теллур	36.9	20.5
Тербий	10.3	5.7
Титан	8.6	4.8
Торий	12	6.7
Тулий	13.3	7.4
Уран	13.9	7.7
Фарфор	3.6-4.5	2.0-2.5
Фенольно-альдегидный полимер без добавок	80	44.4
Фторэтилен пропилен (FEP)	135	75
Хлорированный поливинилхлорид (CPVC)	66.6	37
Хром	6.2	3.4
Цемент	10.0	6.0
Церий	5.2	2.9
Цинк	29.7	16.5
Цирконий	5.7	3.2
Шифер	10.4	5.8
Штукатурка	16.4	9.2
Эбонит	76.6	42.8
Эпоксидная смола , литая резина и незаполненные продукты из них	55	31
Эрбий	12.2	6.8
Этилен винилацетат (EVA)	180	100
Этилен и этилакрилат (EEA)	205	113.9
Эфир виниловый	16 — 22	8.7 — 12

www.dpva.ru